ћинералы и горные породы –оссии и ———–
<<< Ёлементы симметрии
| —одержание | ¬нутреннее
строение кристаллов >>>
ћќ–‘ќЋќ√»„≈— »≈ ќ—ќЅ≈ЌЌќ—“»
ћ»Ќ≈–јЋќ¬
ќ кристаллах и их симметрии
—ингони€, или кристаллографическа€ система
–азбивка 32-х классов симметрии кристаллов на
группы по признаку сходства симметрии приводит к
очень важному дл€ минералогии и кристаллографии
пон€тию сингонии, или кристаллографической
системы. ристаллы одной сингонии
объедин€ютс€ одинаковой совокупностью
характерных углов и наличием одного или
нескольких одинаковых элементов симметрии (в
частности, главной оси или набора осей одного
пор€дка).
¬сего выдел€ют семь (в –оссии) или шесть (за
рубежом) сингонии; в пор€дке повышени€ симметрии
это триклинна€, моноклинна€, ромбическа€,
тетрагональна€, тригональна€ и гексагональна€
(часто, особенно за рубежом, объедин€ютс€ в одну
Ч гексагональную), а также кубическа€
сингонии. ¬ таблице 2ј.1. приведено распределение
32-х классов (видов) симметрии с их названи€ми и
формулами симметрии по семи сингони€м. —вои
названи€ классы симметрии получили по наиболее
характерным дл€ них простым формам; обычно это
так называемые "общие" простые формы
каждого класса.

“аблица 2ј. 1. 32 класса (вида) симметрии
кристаллов
¬ насто€щее врем€ при описании минерала, даже
самом кратком, нар€ду с химической формулой
об€зательно указываетс€ и сингони€, к которой
принадлежат кристаллы минерала; часто
приводитс€ также класс (вид) симметрии. Ёто
св€зано, в частности, с тем, что в качестве
самосто€тельных минеральных видов выдел€ютс€
полиморфные модификации, т.е. минералы, имеющие
одинаковый химический состав, но разную
структуру и, следовательно, симметрию. Ќиже
приводитс€ кратка€ характеристика сингонии (в
пор€дке повышени€ симметрии) Ч их элементов
симметрии, координатных систем (рис. 2ј.7),
морфологических параметров и простых форм.
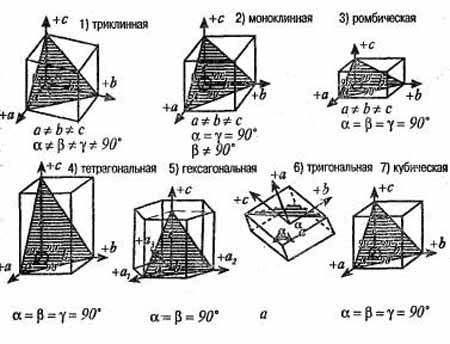
–ис. 2ј.7. ристаллографические
координатные (осевые) системы семи сингоний
1) “риклинна€ сингони€ (включает 2 в.с).
—иноним Ч агарна€ (безосна€). Ёлементы
симметрии либо отсутствуют (не счита€
бесчисленных одинарных осей Lx), либо
представлены только центром инверсии. ¬се
кристаллографические (координатные) оси наклонны;
параметры по всем трем ос€м различны.
ћорфологи€ кристаллов характеризуетс€
отношением параметров а:b:с (причем принимаетс€
b=1) и значени€ми углов a, b, y. ≈динственно возможные
простые формы Ч моноэдры (педионы) и пинакоиды.
2) ћоноклинна€ сингони€ (3 в.с). —иноним Ч моногарна€
(одноосна€). »меетс€ одна двойна€ ось и/или
плоскость симметрии. ѕри их совместном
присутствии они взаимноперпендикул€рны, что
порождает также центр инверсии. ƒвойна€ ось
обычно ориентируетс€ вдоль
кристаллографической оси b, а плоскость
симметрии Ч по нормали к ней (так называема€
моноклинна€ установка). ƒва из трех углов между
координатными ос€ми Ч пр€мые; третий (обычно
угол р) условно выбираетс€ тупым. ѕараметры по
всем трем ос€м различны (a # b # c; a = y = 90∞; b>90∞).
ћорфологические характеристики кристаллов Ч a:b:c
(b принимаетс€ за 1) и величина тупого угла b.
“ипичные простые формы (помимо педионов и
пинакоидов) Ч диэдры (сфеноид, дома) и
(ромбическа€) призма (геометрически это Ч
пр€моугольный параллелепипед).
3) –омбическа€ сингони€ (3 в.с). —иноним Ч дигирна€
(с двойными ос€ми). ¬ наиболее симметричных
кристаллах (планаксиального типа симметрии)
представлены три взаимноперпендикул€рных
двойных оси и три плоскости симметрии,
нормальные к ним, а также центр инверсии. ¬ менее
симметричных кристаллах могут присутствовать
только три двойных оси (аксиальный тип симметрии)
либо одна пол€рна€ двойна€ ось и две проход€щие
через нее взаимно-перпендикул€рные плоскости
(планальный тип симметрии). ¬се три угла между
кристаллографическими ос€ми Ч пр€мые, но сами
оси по-прежнему неравнозначны (a # b # c; a = y = 90∞).
ћорфологической характеристикой кристаллов
служит только осевое отношение a:b:c, где b
приравниваетс€ к 1. “ипичные простые формы
(помимо педионов и пинакоидов) Ч ромбические
призмы, пирамиды и бипирамиды, а также
ромбический тетраэдр (бисфеноид).
“риклинна€, моноклинна€ и ромбическа€ сингонии
составл€ют группу низших сингонии; они
охватывают 8 классов симметрии, относ€щихс€ к
низшей категории по уровню симметрии. ¬ этой
группе отсутствуют оси более высокого пор€дка,
нежели двойные.
—ледующие три сингонии Ч тетра-, три- и
гексагональна€ Ч вход€т в группу средних
сингонии; к ним принадлежат 10 классов
симметрии, относ€щихс€ к средней категории по
уровню симметрии и характеризующихс€ наличием
одной оси высокого пор€дка Ч 3-го, 4-го или 6-го
(включа€ инверсионные). ѕричем, поскольку простые
формы в гексагональной и тригональной сингони€х
(и только в них) в значительной мере
перекрываютс€, обе они нередко (особенно за
рубежом) объедин€ютс€ в одну гексагональную, а
тригональна€ рассматриваетс€ как подсистема
гексагональной. Ётим обусловлено расхождение в
общем числе сингонии: 6 или 7 у разных авторов.
4) “етрагональна€ (квадратна€, тетрагирна€) сингони€
(7 в.с). »меетс€ одна ось симметрии 4-го пор€дка
(проста€ или инверсионна€), ориентированна€
вертикально Ч вдоль кристаллографической оси с.
¬ наиболее высокосимметричном классе
(планаксиальный тип симметрии) нар€ду с
четверной присутствуют 4 двойных оси,
перпендикул€рные ей, 5 плоскостей симметрии,
перпендикул€рных п€ти ос€м, и центр инверсии (но
не в кристаллах с осью L4i).
¬ других классах число элементов симметрии
существенно уменьшаетс€, но наличие четверной
оси об€зательно. ќна может быть пол€рной,
бипол€рной или инверсионной; пол€рна€ или
инверсионна€ оси могут сопровождатьс€ другими
элементами симметрии (в первом случае Ц в
планальном типе симметрии Ч четырьм€
плоскост€ми, проход€щими через нее; во втором Ч в
инверсионно-планальном типе Ч двум€ двойными
ос€ми, ей перпендикул€рными, и двум€ плоскост€ми,
проход€щими через нее), но могут и не
сопровождатьс€, т.е. €вл€тьс€ единственным
элементом симметрии кристалла (в примитивном и
инверсионно-примитивном типах симметрии).
¬ центральном типе симметрии нар€ду с
бипол€рной осью 4-го пор€дка присутствуют
нормальна€ к ней плоскость и центр инверсии, в
аксиальном типе имеютс€ только п€ть осей
симметрии: одна бипол€рна€ 4-го и четыре
(перпендикул€рные ей) второго пор€дка. ¬
тетрагональной сингонии a = b # c, a = у = 90∞).
ћорфологической характеристикой кристаллов
служит отношение ах. “ипичные простые формы Ч тетрагональные
(четырехгранные, с квадратным поперечным
сечением) и дитетрагональные (восьмигранные,
с поперечным сечением в виде правильного
восьмиугольника) призмы, бипирамиды и пирамиды,
а также тетрагональный тетраэдр (бисфеноид), тетрагональный
трапецоэдр (его грани представлены трапецами,
от греческого "трапеза" Ч стол; не путать с
трапеци€ми!; так в кристаллографии именуют
четырехугольники с одной парой равных соседних
сторон) и тетрагональный скаленоэдр (его
грани имеют форму разносторонних треугольников
Ч скаленов, от греческого "скаленос" Ч
косой). ¬ некоторых классах по-прежнему возможны пинакоиды
и педионы, в частности базопинакоиды в
комбинации с призмами и педион (моноэдр) как
основание (базальна€ грань) пирамиды.
¬сего в тетрагональной сингонии известно 9
простых форм.
5) “ригональна€ (тригирна€) сингони€ (5
или 7 классов симметрии). ƒва класса симметрии, в
которых присутствует шестерна€ инверсионна€
ось (равнозначна€, как мы уже знаем, сочетанию
обычной тройной оси с перпендикул€рной к ней
плоскостью симметрии), относ€т то к тригональной,
то к гексагональной сингонии, что подчеркивает
известную условность их разделени€ и отсутствие
между ними четко выраженной границы. ¬прочем,
среди минералов представителей обоих этих
классов почти нет.
¬ этой сингонии (равно как и в гексагональной)
координатна€ система четырехосна€; три оси,
обозначаемые буквой а (а1, а2 и а3),
эквивалентны и располагаютс€ в горизонтальной
плоскости под углом 120∞ друг к другу, а четверта€
(с) вертикальна, т.е. перпендикул€рна трем
остальным. ѕо оси с ориентируетс€ тройна€ ось
тригональных кристаллов, наличие которой дл€ них
об€зательно и служит отличительным признаком
тригональной сингонии.
роме нее могут присутствовать двойные оси
(до трех), зеркальные плоскости (до 3-х или Ч в
кристаллах с шестерной инверсионной осью Ч 4-х) и
иногда центр инверсии. “ройна€ ось может быть
пол€рной или бипол€рной (вспомним, что
инверсионна€ тройна€ ось равнозначна сочетанию
простой тройной оси с центром инверсии).
’арактеристикой морфологии кристаллов служит
отношение с:а, которое может быть и больше, и
меньше единицы (а # с). —имволы простых форм
тригональной сингонии, ввиду четырех-осности
координатной системы, состо€т из четырех
индексов: (hkil), где i = -(h+k).
ѕомимо установки, общей дл€ гексагональной и
тригональной сингонии (с четырьм€ координатными
ос€ми), дл€ тригональных кристаллов, особенно
ромбоэдрических изометричного облика, иногда
принимаетс€ друга€ установка Ч ромбоэдрическа€,
с трехосной системой координат, в которой
кристаллографические оси направлены вдоль трех
ребер так называемого основного ромбоэдра (1011),
пересекающихс€ на тройной оси.
–омбоэдр Ч восьмивершинник с формулой
симметрии L33L23PC, получаемый
раст€жением или сжатием куба (гексаэдра) вдоль
одной из его четырех тройных осей; все грани
ромбоэдра имеют форму одинаковых ромбов. ¬ этой
установке все углы между ос€ми равны, но отличны
от пр€мого (а = b = у # 90∞). «а единичную грань
принимают грань пинакоида или моноэдра,
перпендикул€рную тройной оси; при этом все ее
линейные параметры оказываютс€ одинаковыми (а = b
= с). ’арактерной морфологической константой
кристаллов становитс€ угол между координатными
ос€ми, т.е. угол а основного ромбоэдра .
ѕростые формы тригональной сингонии:
тригональные (трехгранные) и дитригональные
(шестигранные) призмы, бипирамиды и пирамиды,
ромбоэдры, тригональный трапецоэдр и
тригональный (дитригональный) скаленоэдр;
возможны также педион и пинакоид.
6) √ексагональна€ (гексагарна€) сингони€
(7 или 5 классов симметрии; см. сноску 8).
ќтличительна€ особенность кристаллов Ч
присутствие одной вертикальной оси 6-го пор€дка
(совмещенной с координатной осью с). Ўестерна€
ось может быть бипол€рной и пол€рной; два класса
симметрии, в которых она €вл€етс€ инверсионной,
нередко относ€т к тригональной сингонии
(поскольку, как мы знаем, ось L6i приводитс€ к
простой тройной оси в сочетании с
перпендикул€рной плоскостью симметрии).
ѕомимо шестерной оси могут присутствовать двойные
оси (до 6), зеркальные плоскости (тоже до 6) и
иногда центр инверсии (только не в кристаллах
с осью L6i). —истема координат
Ч четырехосна€; символы граней включают 4
индекса; морфологической характеристикой
кристаллов служит отношение с:а. ѕростые формы:
гексагональные (6-гранные) и дигексагональные
(12-гранные) призмы, бипирамиды, пирамиды, а также
гексагональный трапецоэдр (с 12-ю гран€ми Ч по 6
сверху и снизу). ¬ажно отметить отсутствие
ромбоэдра Ч наиболее характеристической формы
тригональной сингонии; отсутствует и скаленоэдр.
¬сего в гексагональной и тригональной сингони€х
в сумме насчитываетс€ 16 простых форм.
7) убическа€ (изометрическа€,
правильна€) сингони€ (5 классов симметрии) Ч
сама€ высокосимметрична€, единственна€,
относ€ща€с€ к высшей категории по уровню
симметрии. ƒл€ принадлежащих к ней кристаллов
об€зательно наличие четырех
взаимноперпендикул€рных осей 3-го пор€дка
(которые обычно бипол€рны, но в одном из классов,
отвечающем примитивному типу симметрии,
€вл€ютс€ пол€рными). Ќар€ду с ними в трех классах
(представл€ющих аксиальный, планальный и
планаксиальный типы симметрии) имеютс€ три
четверных оси (в классе с планальным типом
симметрии они инверсионные). ќбычно (за
исключением того же класса) присутствуют 3 или 6
двойных осей. ¬ трех классах из п€ти есть
плоскости симметрии (3, 6 или 9) и в двух из них Ч
центр инверсии.
—истема координат Ч обычна€ трехосна€, со
взаимно-перпендикул€рными ос€ми (параллельными
ребрам куба); параметры по всем трем ос€м равны,
т.е. их отношение имеет вид 1:1:1. роме того, углы
между соответствующими гран€ми простых форм
кубической сингонии посто€нны дл€ всех
кристаллов, к ней относ€щихс€, и не могут служить
диагностическими или отличительными признаками
минералов. “аким образом, кристаллы кубической
сингонии лишены какой-либо специфической
морфологической характеристики; их прин€то
характеризовать величиной параметра кубической
элементарной €чейки (т.е. длиной ребра
элементарного куба) а0, очень легко и просто
определ€емого непосредственно по
рентгенограмме порошка минерала. «ато простые
формы кубической сингонии весьма специфичны: ни
одна из них в других сингони€х не встречаетс€.
¬сего в этой сингонии 15 простых форм (все Ч закрытые):
тетраэдр (4-гранник); куб, или гексаэдр (6-гранник);
октаэдр (8-гранник); п€ть 12-гранников Ч
ромбододекаэдр, пентагон-додекаэдр,
тригонтритетраэдр (триакис-тетраэдр),
тетрагон-тритетраэдр (дельтоэдр),
пентагон-тритетраэдр; шесть 24-гранников Ч
тригон-триоктаэдр (триакис-октаэдр),
тетрагон-триоктаэдр (икоситетраэдр),
пентагон-триоктаэдр (гироэдр), тетрагексаэдр,
гексатетраэдр, дидодекаэдр; и единственный
48-гранник Ч гексоктаэдр.
ѕростые формы низжих сингоний изображены на
рис. 2ј8, средних сингоний Ч на рис. 2ј.9 и
кубической сингонии на рис. 2ј.10.
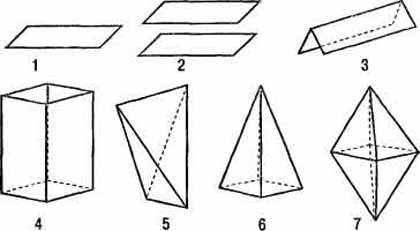
–ис. 2ј.8. ѕростые формы низших сингоний:
1 Ч моноэдр; 2 Ч пинакоид; 3 Ч диэдр; 4 Ч
ромбическа€ призма; 5 Ч ромбический тетраэдр; 6 Ч
ромбическа€ пирамида; 7 Ч ромбическа€
бипирамида;
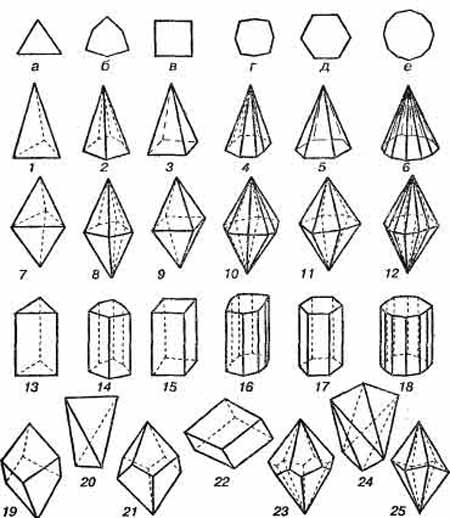
–ис. 2ј.9. ѕростые формы средних
сингоний: пирамиды: 1 Ч тригональна€; 2 Ч
дитригональна€; 3 Ч тетрагональна€; 4 Ч
дитетрагональна€; 5 Ч гексагональна€; 6 Ч
дигексагональна€; бипирамиды: 7 Ч тригональна€; 8
Ч дитригональна€; 9 Ч тетрагональна€; 10 Ч
дитетрагональна€; 11 Ч гексагональна€; 12 Ч
дигексагональна€; призмы: 13 Ч тригональна€; 14 Ч
дитригональна€; 15 Ч тетрагональна€; 16 Ч
дитетрагональна€; 17 Ч гексагональна€; 18 Ч
дигексагональна€; 19 Ч тригональный трапецоэдр; 20
Ч тетрагональный тетраэдр; 21 Ч тетрагональный
трапецоэдр; 22 Ч ромбоэдр; 23 Ч гексагональный
трапецоэдр; 24 Ч тетрагональный скаленоэдр; 25 Ч
тригональный скаленоэдр. ¬верху изображены
формы оснований и сечений, перпендикул€рных
главной сии: а Ч тригон; б Ч дитригон; в Ч
тетрагон; г Ч дитетрагон; д Ч гексагон; е Ч
дигексагон.
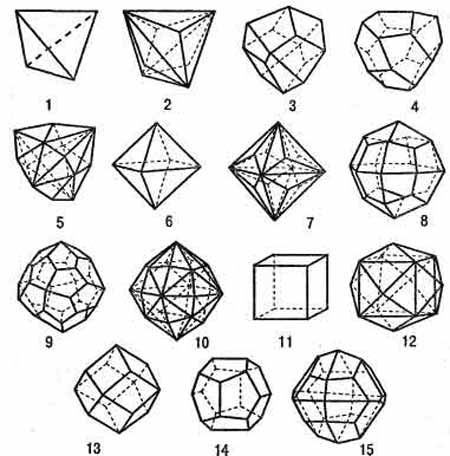
–ис. 2ј.10. ѕростые формы кубической
сингонии: 1 Ч тетраэдр; 2 Ч тригон-тритраэдер; 3 Ч
тетрагон-тритетраэдр; 4 Ч пентагон-тритетраэдр; 5
Ч гексатетраэдр; 6 Ч октаэдр; 7 Ч
тригон-триоктаэдр; 8 Ч тетрагон-триоктаэдр; 9 Ч
пентагон-триоктаэдр; 10 Ч гексоктаэдр; 11 Ч
гексаэдр; 12 Ч тетрагексаэдр; 13 Ч ромбододекаэдр;
14 Ч пентагон-додекаэдр; 15 Ч дидодекаэдр.
Ќесколько дополним и расширим характеристику
классов симметрии и простых форм. ¬ каждой
сингонии один из вход€щих в нее классов обладает максимальной
(дл€ данной сингонии) симметрией, т.е. наибольшим
числом элементов симметрии, и носит название нормального,
или голоэдрического. нему принадлежит
сама€ богата€ гран€ми в данной сингонии проста€
форма, котора€ называетс€ полногранной и
считаетс€ общей формой голоэдрического класса Ч
голоэдром.
¬ триклинной сингонии голоэдрический
(пинакоидальный) класс относитс€ к центральному
типу симметрии, во всех остальных сингони€х
голоэдрическими €вл€ютс€ классы планаксиального
типа симметрии. –аспределение классов (видов)
симметрии по ступен€м (типам) симметрии в рамках
каждой сингонии представлено в таблице 2ј.2.
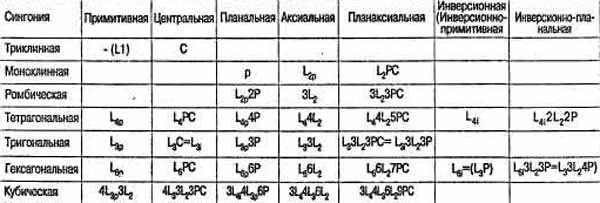
“аблица 2ј.2. –аспределение видов
(классов) симметрии по ступен€м (типам) симметрии
дл€ всех сингоний.
»з голоэдрического класса вывод€тс€ остальные
классы соответствующей сингонии путем
последовательного (ступенчатого) снижени€
симметрии, что достигаетс€ сокращением числа
граней полногранных форм сначала вдвое, а затем
вчетверо (т.е. еще раз вдвое). “акого рода операции
называютс€ мероэдрическими (от греческого
"мерос" Ч часть), а выводимые с их помощью
простые формы с уменьшенным числом граней (в
зависимости от ступени сокращени€) Ч гемиэдрическими
(перва€ ступень: формы с половинным числом
граней) и тетартоэдрическими (втора€ ступень:
формы с четвертью исходного числа граней). ¬
гексагональной и тригональной сингони€х
возможна (в единственном случае) и треть€ ступень
сокращени€ числа граней, привод€ща€ к огдоэдрии
Ч уменьшению количества граней в 8 раз; при этом
возникает класс примитивной симметрии с одним
элементом симметрии Ч тройной пол€рной осью.
ћероэдрические операции в низших, средних и
кубической сингони€х осуществл€ютс€ разными
способами; но привод€т они в конечном счете к
классам (и соответствующим простым формам)
аксиальной, планальной, центральной и, наконец
сингонии примитивна€ симметри€ достигаетс€ уже
при гемиэдрическом превращении пинакоидов в
моноэдры).
¬ ходе мероэдрических операций возможны
различные варианты. “ак, при переходе к классам аксиальной
симметрии (в кристаллах присутствуют только
простые поворотные оси и нет центра инверсии) мы
сталкиваемс€ с €влением энантиоморфизма
(греческое "энантиос" Ч обратный,
противоположный): возникают пары зеркально
равных фигур, относ€щихс€ друг к другу как
зеркальные изображени€ (подобно правой и левой
рукам). ” таких энантиоморфных кристаллов
различают правую и левую разновидности, которые
могут быть совмещены путем отражени€ в
зеркальной плоскости (но не путем поворота
вокруг оси симметрии).
ѕравые и левые разновидности известны,
например, дл€ таких простых форм, как сфеноид
(осевой диэдр) в моноклинной и ромбический тетраэдр
(бисфеноид) Ч в ромбической сингонии,
тетрагональный, тригональный и гексагональный
трапецоэдры, тригональна€ бипирамида,
дитригональна€ пирамида, ромбоэдр Ч в
средних сингони€х и, наконец, пентагон-триоктаэдр
(гироэдр) Ч в кубической сингонии.
ƒостаточно присутстви€ на кристаллах
минералов, принадлежащих к гемиэдрическим
классам с аксиальной симметрией, граней
перечисленных выше простых форм, чтобы по ним
можно было различить правую и левую
энантиоморфные разновидности; так, например,
правый и левый кварц (рис. 2ј.11)
различаютс€ по положению граней энантиоморфных
фигур Ч тригонального трапецоэдра и/или
тригональной бипирамиды (если, конечно, они
наблюдаютс€ на кристаллах, что бывает далеко не
всегда). √емиэдрическое преобразование вообще
может затронуть только общую форму голоэдрического
класса (голоэдр), не каса€сь других простых форм;
но дл€ возникновени€ пары энантиоморфных
разновидностей и этого достаточно (например, из
ромбической бипирамиды получаютс€ два
бисфеноида Ч правый и левый ромбические
тетраэдры).
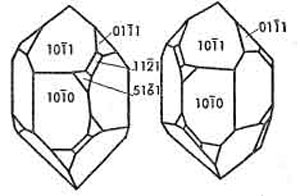
–ис. 2ј.11. ѕравый (а) и левый (б) кристаллы кварца.
ѕростые формы: (1011) и (0111 ) Ч ромбоэдры 1-го и 2-го
рода; (0111 ) Ч тригональна€ бипирамида (права€ и
лева€); (1121) Ч тригональный трапецоэдр (правый и
левый)
≈сли же мероэдрические операции привод€т к
классам планальной или центральной симметрии, то
вместо энантиоморфных разновидностей
гемиэдрических простых форм возникают конгруэнтные
(совместимые при вращении) пары; они
совмещаютс€ путем поворота около двойной оси
симметрии. Ёти пары различаютс€ по ориентировке
относительно координатных осей: одна форма Ч та,
единична€ грань которой пересекает только
положительные направлени€ осей, Ч считаетс€ положительной
и обозначаетс€ знаком "+", а друга€, у которой
единична€ грань пересекает отрицательное
направление хот€ бы одной из осей, Ч отрицательной
(со знаком "-").
ак и в геометрической системе координат,
положительный конец X (а) обращен вперед (на
зрител€), отрицательный назад; положительное
направление оси Y (b) Ч вправо, отрицательное
Ч влево, а оси Z (с): положительное Ч вверх,
отрицательное Ч вниз. ѕоложительным
€вл€етс€ верхний правый октант трехосной
системы координат.
“аких положительных и отрицательных форм в
гемиэдрических и тетраэдрических классах очень
много. Ќа кристаллах они могут присутствовать одновременно
и, что интересно, в некоторых случа€х (хот€ отнюдь
не всегда) их можно различить по внешнему виду.
Ќапример, у минерала халькопирита
CuFeS2 грани положительного тетрагонального
тетраэдра (бисфеноида) покрыты штриховкой или
матовые, а грани отрицательного Ч гладкие,
блест€щие. ѕоложительный тетраэдр кубического
минерала сфалерита ZnS визуально
отличаетс€ от отрицательного различной
структурой граней (более четкие бугорки роста на
гран€х положительного тетраэдра), фигурами
травлени€ (обычно отсутствующими на гран€х
отрицательного тетраэдра), а также частым
закономерным нарастанием халькопирита только на
грани положительного тетраэдра сфалерита.
¬ гемиэдрических классах планальной
симметрии ромбической и средних сингонии, где в
ацентричньгх кристаллах присутствуют только
пол€рные оси и проход€щие через них плоскости
симметрии, в результате одной из мероэдрических
операций, состо€щей в сокращении числа граней
вдвое путем ликвидации верхней или нижней частей
голоэдра, с преобразованием бипирамид в пирамиды,
возникают гемиэдрические формы Ч верхн€€ и
нижн€€ пирамиды, причем кажда€ из них может быть
положительной и отрицательной.
Ќесовпадение огранени€ этих пирамид на обоих
концах одного и того же кристалла может служить
€рким выражением гемиморфизма, о котором
упоминалось выше и который про€вл€етс€ только в
кристаллах гемиэдрических классов. ѕомимо
тригональных турмалина и кварца, хорошим примером тут может
служить ромбический минерал гемиморфит (каламин) Zn4Si2O7(OH)2
Х H2O; в самом его названии заключено
указание на гемиморфный облик кристаллов.
’арактеризу€ простые формы средних
сингоний, нужно еще упом€нуть, что на кристаллах,
к ним относ€щихс€, могут по€вл€тьс€ грани призм,
пирамид, бипирамид, ромбоэдров,
тетрагональных тетраэдров 1-го, 2-го и 3-го
рода. ќдноименные простые формы разного рода
различаютс€ только по ориентировке относительно
кристаллографических осей (т.е. по символам
граней), а по внешнему виду обычно неотличимы (см.
рис. 2ј.11). —реди них (кроме призм) могут
встречатьс€ положительные и отрицательные,
а также энантиоморфные разновидности.
<<< Ёлементы симметрии
| —одержание | ¬нутреннее
строение кристаллов >>>
ѕознакомитьс€ с изображени€ми и описани€ми других объектов природы –оссии и сопредельных стран -
 минералов и горных пород, минералов и горных пород,
 почв, почв,
 грибов, грибов,
 водорослей, водорослей,
 лишайников, лишайников,
 листостебельных мхов, листостебельных мхов,
 деревьев, кустарников, кустарничков и лиан, деревьев, кустарников, кустарничков и лиан,
 трав€нистых растений (цветов), трав€нистых растений (цветов),
 €год и других дикорастущих сочных плодов, €год и других дикорастущих сочных плодов,
 водных беспозвоночных животных, водных беспозвоночных животных,
 насекомых-вредителей леса, насекомых-вредителей леса,
 дневных бабочек, дневных бабочек,
 пресноводных и проходных рыб, пресноводных и проходных рыб,
 земноводных (амфибий), земноводных (амфибий),
 пресмыкающихс€ (рептилий), пресмыкающихс€ (рептилий),
 птиц, птичьих гнезд, их €иц и голосов, а также птиц, птичьих гнезд, их €иц и голосов, а также
 млекопитающих (зверей), -
можно в разделе ѕрирода –оссии нашего сайта. млекопитающих (зверей), -
можно в разделе ѕрирода –оссии нашего сайта.
¬ разделе ѕрирода в фотографи€х
размещены также тыс€чи научных фотографий грибов, лишайников, растений и
животных –оссии и стран бывшего ———–, а в разделе
ѕриродные ландшафты мира - фотографии природы
 ≈вропы, ≈вропы,
 јзии, јзии,
 —еверной и —еверной и
 ёжной јмерики, ёжной јмерики,
 јфрики, јфрики,
 јвстралии и Ќовой «еландии и јвстралии и Ќовой «еландии и
 јнтарктики. јнтарктики.
¬ разделе ћетодические материалы
¬ы также можете познакомитьс€ с описани€ми разработанных экологическим центром "Ёкосистема"
печатных определителей растений средней полосы,
карманных определителей объектов природы средней полосы,
определительных таблиц "√рибы, растени€ и животные –оссии",
компьютерных (электронных) определителей природных объектов,
полевых определителей дл€ смартфонов и планшетов,
методических пособий по организации проектной де€тельности школьников и полевых экологических исследований
(включа€ книгу дл€ педагогов " ак организовать полевой экологический практикум"), а также
учебно-методических
фильмов по организации проектной исследовательской де€тельности школьников в природе.
ѕриобрести все эти материалы можно в нашем некоммерческом »нтернет-магазине.
“ам же можно приобрести mp3-диски √олоса птиц средней полосы –оссии и
√олоса птиц –оссии, ч.1: ≈вропейска€ часть, ”рал, —ибирь.
|







