ћинералы и горные породы –оссии и ———–
<<< √еометрические
формы кристаллов | —одержание
| —ингони€, или кристаллографическа€
система >>>
ћќ–‘ќЋќ√»„≈— »≈ ќ—ќЅ≈ЌЌќ—“»
ћ»Ќ≈–јЋќ¬
ќ кристаллах и их симметрии
Ёлементы симметрии
√рани (ребра, вершины) кристалла св€заны между
собой элементами симметрии Ч воображаемыми
лини€ми и плоскост€ми, проход€щими через центр
кристалла, а также особой точкой, расположенной в
его центре.
¬ макроскопической кристаллографии различают три
вида элементов симметрии: оси симметрии (или
поворотные оси), (зеркальные) плоскости симметрии
(плоскости отражени€) и центр симметрии, или
центр инверсии Ч точку, наход€щуюс€ в центре
некоторых кристаллов. ¬ кристаллах могут
существовать оси симметрии 1-го (одинарные), 2-го
(двойные), 3-го (тройные), 4-го (четверные) и 6-го
(шестерные) пор€дка.
ќдинарные оси называютс€ также "ос€ми
идентичности", так как дл€ того, чтобы
поворотом вокруг такой "оси" достичь
положени€, идентичного исходному, угол поворота
должен составить 360∞; иными словами, кристалл
должен быть повернут вокруг себ€ на 360∞ и снова
приведен в первоначальное положение, т.е. ' ось
идентичности" по существу вовсе не €вл€етс€
осью симметрии: в любом кристалле, даже самом
низкосимметричном, таких "осей" Ч
бесконечное множество, и если симметри€
кристалла описываетс€ цифрой 1 (обозначение
одинарной оси), то это означает отсутствие вс€кой
симметрии; огранение подобного кристалла
состоит из одних моноэдров (педионов).
ѕри наличии двойной оси кристалл приводитс€ в
положение, идентичное исходному, уже поворотом
на 180∞ (этот поворот прин€то осуществл€ть против
часовой стрелки), при наличии тройной оси Ч
поворотом на 120∞, четверной оси Ч на 90∞ и
шестерной Ч на 60∞. ќсь 5-го пор€дка в кристаллах
практически не реализуетс€, в частности по той
причине, что равносторонние правильные
п€тиугольники не могут целиком без зазоров
заполнить плоскость, а соответствующие объемные
фигуры Ч пространство; между тем, в живой природе
п€терна€ симметри€ весьма распространена
(вспомним хот€ бы множество видов цветов с
п€тилепестковыми венчиками-звездочками или
п€тилучевые морские звезды). Ќедаром же академик
Ќ.¬.Ѕелов Ч глава отечественной школы
структурной кристаллографии и кристаллохимии
минералов Ч называл п€терную симметрию "симметрией
жизни"!
„исло элементов симметрии в кристаллах может
быть очень разным Ч в зависимости от степени
симметрии кристаллического многогранника. “ак, в
кубе Ч наиболее симметричной фигуре Ч
одновременно присутствуют 23 элемента симметрии:
9 плоскостей (3 Ч параллельные гран€м и 6 Ч
проход€щие через их верных, 4 тройных и 6 двойных)
и центр инверсии (который, естественно, может
быть в кристалле только один).
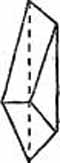 — другой стороны, в
наименее симметричных кристаллах элементы
симметрии (кроме одинарных осей) вообще
отсутствуют. ¬прочем, такой пример известен в
мире минералов всего лишь один: это кристаллы
бората парахилгардита —а2¬5ќ9—1
Х H2ќ (рис. 2ј.5), ограниченные симметрии
кристалла, тем больше в нем присутствует
различных элементов симметрии (хот€ известны и
частные отклонени€ от этого правила). — другой стороны, в
наименее симметричных кристаллах элементы
симметрии (кроме одинарных осей) вообще
отсутствуют. ¬прочем, такой пример известен в
мире минералов всего лишь один: это кристаллы
бората парахилгардита —а2¬5ќ9—1
Х H2ќ (рис. 2ј.5), ограниченные симметрии
кристалла, тем больше в нем присутствует
различных элементов симметрии (хот€ известны и
частные отклонени€ от этого правила).
–ис. 2ј.5. јсимметричный кристалл минерала
парахилгардита
¬ращение вокруг оси симметрии, отражение в
плоскости симметрии и перенос (инверси€) через
центр симметрии Ч фактически отражение в
зеркальной точке, расположенной в центре
кристалла, Ч все такие действи€ называютс€
операци€ми симметрии, или симметричными
(симметрическими) преобразовани€ми. Ёто
простые операции симметрии; кроме них в
кристалле возможны и более сложные Ч
комбинированные, или составные симметричные
преобразовани€: одновременный поворот вокруг
оси и отражение либо в плоскости симметрии
(операци€ с так называемой зеркальной, или
зеркально-поворотной осью), либо в центре
инверсии (операци€ с инверсионной осью).
¬сего, с учетом подобных операций, в кристаллах
возможно 10 основных симметричных
преобразований; однако в большинстве случаев
такие дополнительные элементы симметрии как
зеркальные и инверсионные оси могут быть
заменены комбинаци€ми основных элементов
симметрии Ч поворотных осей с зеркальными
плоскост€ми или центром инверсии (причем
последний может и не про€витьс€ в кристаллах с
инверсионными ос€ми как самосто€тельный
элемент симметрии: в частности, в кристаллах с
четверной и шестерной инверсионными ос€ми, Ч а
только с ними практически и приходитс€
сталкиватьс€, Ч он всегда отсутствует).
Ќапример, двойна€ инверсионна€ ось равнозначна
плоскости симметрии, ей перпендикул€рной,
тройна€ Ч комбинации простой тройной оси и
центра инверсии; шестерна€ Ч тройной оси и
перпендикул€рной ей плоскости симметрии.
»сключение составл€ет 4-на€ инверсионна€ (она
же зеркальна€) ось, котора€, впрочем, реально
установлена в достаточно чистом виде лишь в
кристаллах очень немногих минералов: эта ось
всегда совпадает с простой двойной осью
симметрии (при отсутствии центра инверсии), но
отнюдь не вс€ка€ двойна€ ось в отсутствие центра
инверсии €вл€етс€ четверной инверсионной.
÷ентр инверсии присутствует в кристаллах
далеко не всех минералов; если его нет, то
кристаллы называютс€ "нецентросимметричными",
или (что проще) "ацентричными". ƒл€ таких
кристаллов (типичные примеры Ч кристаллы кварца или турмалина)
характерно €вление гемиморфизма:
противоположные концы хорошо образованных
кристаллов приобретают разное огранение.
¬ гемиморфных кристаллах оси симметрии
соедин€ют различные элементы огранени€:
например, исход€ из вершины пирамиды, ось
упираетс€ в грань (моноэдр), служащую ее
основанием. “акие оси называют пол€рными, в
отличие от бипол€рных (обычных) осей, проход€щих
через центр симметрии и соедин€ющих одинаковые
элементы огранени€. ћногие свойства кристаллов
на противоположных концах пол€рных осей
мен€ютс€ на обратные; дл€ гемиморфных кристаллов
типично про€вление линейного
пьезоэлектрического, пироэлектрического,
трибо-электрического, иногда и
сегнетоэлектрического эффектов, т.е. они электризуютс€,
приобрета€ на противоположных концах разные по
знаку зар€ды как при механическом, так и при
термическом воздействии (в том числе при трении
Ч трибоэффект) или даже, как сегнетоэлектрики,
самопроизвольно (в некотором температурном
интервале). ѕол€рные оси обозначаютс€ так же, как
и обычные (бипол€рные), но с добавлением к
цифровому индексу буквы р: L2p, L3p, L4p,
L6p.
¬вед€ пон€ти€ об элементах и операци€х
симметрии в кристаллах, можно дать более строгое
определение кристаллографической простой
формы: простой формой называетс€ совокупность
граней кристалла, св€занных между собой
каким-либо элементом симметрии и вывод€щихс€
одна из другой ("размножающихс€")
посредством соответствующей операции симметрии.
ристаллы каждого минерала характеризуютс€
определенным и посто€нным набором элементов
симметрии. «амечательно при этом, что зачастую
кристаллы одного и того же минерала могут быть
совсем непохожи друг на друга по внешнему облику,
могут даже очень резко различатьс€
относительным развитием простых форм,
приобрета€ то столбчатую, то пластинчатую, то
изометричную или какую-либо иную форму, Ч но
комплекс присущих им элементов симметрии не
претерпевает никаких изменений (закон
посто€нства симметрии).
Ётот комплекс, характеризующий кристалл и его
симметрию, прин€то записывать в виде так
называемой кристаллографической формулы,
или формулы симметрии. ¬ ней сначала
привод€тс€ обозначени€ осей (обычно в
последовательности, отвечающей убывающему
пор€дку) с указанием их количества, затем
записываетс€ число плоскостей и в заключение
отмечаетс€ наличие центра инверсии.
Ќапример, формула симметрии куба 3L44L36L29PC
(в подобных формулах используетс€ именно така€
система обозначений, но — нередко замен€етс€ на z
); она расшифровываетс€ следующим образом:
(кубический) кристалл имеет 3 четверных оси, 4
тройных, 6 двойных, 9 зеркальных плоскостей и
центр инверсии Ч итого, как мы уже знаем, 23
элемента симметрии.
Ќеобходимо подчеркнуть, что одна и та же
формула симметрии характеризует не какой-либо
единственный кристалл или вид кристаллов, а все
виды кристаллов, имеющие одинаковую с ним
симметрию, т.е. относ€щиес€ к одному классу
симметрии (см. ниже). ‘актически, привод€ при
описании минерала формулу симметрии его
кристаллов, мы тем самым сразу же определ€ем их
принадлежность к тому или иному классу
симметрии, что весьма существенно дл€
диагностики минерала.
—очетание, или, как говор€т кристаллографы,
"сложение" элементов симметрии в
кристаллах не произвольно, а подчин€етс€
определенным правилам, ограничивающим число
возможных комбинаций (в противном случае, при
наличии в кристаллах семи независимых элементов
симметрии, оно было бы огромным). —уть этих
ограничений, налагаемых правилами сложени€
элементов симметрии, заключаетс€ в том, что,
во-первых, некоторые операции симметрии
оказываютс€ равнозначными, а во-вторых,
симметричные преобразовани€ действуют и на сами элементы
симметрии. ѕоследнее обсто€тельство приводит
к тому, что одни элементы симметрии порождают
(генерируют) другие, а это значит, что если,
например, в кристалле имеютс€ две пересекающихс€
двойных оси, то в нем об€зательно по€вл€ютс€ и
оси пересечени€ двойных осей; все эти оси
располагаютс€ перпендикул€рно двум
исходным. ¬сего таких правил шесть. Ѕлагодар€ им
число возможных видов, или классов, симметрии
кристаллов, т.е. простых комбинаций элементов
симметрии, выражаемых различными формулами
симметрии, резко сокращаетс€.
—уществует строгий вывод этих видов (классов)
симметрии, но здесь достаточно сказать, что их
насчитываетс€ дл€ кристаллов 32. ѕожалуй,
стоит еще сообщить, какие положени€ легли в
основу вывода 32-х классов симметрии кристаллов и
соответствующих им 47 простых форм. ѕри этом
выводе оказалось удобным использовать
представление о п€ти ступен€х (типах)
симметрии кристаллов. Ќиже они перечислены в
пор€дке повышени€ симметрии (применительно к низкосимметричным
кристаллам); см. также рис. 2ј.6.
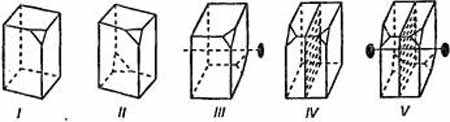
–ис. 2ј.6. ќсновные ступени симметрии
- 1-€ ступень. ѕримитивна€ (пол€рна€) симметри€:
элементы симметрии (кроме осей идентичности)
отсутствуют. ¬се грани Ч самосто€тельные
простые формы Ч моноэдры (педионы), и ни одна из
них не повтор€етс€.
- 2-€ ступень. ÷ентральна€ симметри€:
единственный элемент симметрии Ч центр
инверсии. ѕротиволежащие грани попарно равны и
антипараллельны (т.е. повернуты в
противоположные стороны); така€ проста€ форма
называетс€ пинакоидом.
- 3-€ ступень. јксиальна€ (осева€) симметри€:
присутствует одна пол€рна€ ось 2-го пор€дка.
Ћюбые две грани совмещаютс€ путем поворота
вокруг этой оси на 180∞, образу€ клиновидную
простую форму Ч сфеноид (осевой диэдр).
- 4-€ ступень. ѕланальна€ симметри€: имеетс€
зеркальна€ плоскость, дел€ща€ пополам телесный
угол между двум€ гран€ми, которые располагаютс€
в виде двускатной крыши и совмещаютс€ между
собой путем отражени€ в плоскости симметрии.
Ќазвание такой простой формы Ч дома (безосный,
или плоскостной диэдр) 3\
- 5-€ ступень. ѕланаксиальна€ симметри€:
сочетание двух (точнее трех) предыдущих ступеней.
ƒвойна€ ось становитс€ бипол€рной (присутствует
центр инверсии); зеркальна€ плоскость
перпендикул€рна ей. ’арактерна€ проста€ форма Ч
четырехгранна€ призма.
ѕо€вление инверсионных осей вместо простых
поворотных увеличивает число ступеней симметрии
до семи: добавл€ютс€ еще две ступени Ч инверсионна€
(или инверсионно-примитивна€) и инверсионно-планальна€.
»х представители в мире минералов встречаютс€,
впрочем, редко.
¬ дальнейшем, зна€, какие в кристаллах возможны оси
симметрии, их последовательно сочетают с
каждой из перечисленных выше ступеней симметрии
и таким путем приход€т к 32 точечным группам,
соответствующим отдельным видам (классам)
симметрии, т.е. всем возможным комбинаци€м
элементов симметрии в кристаллах.
¬ основе введенного √есселем термина "точечные
группы" лежит то обсто€тельство, что в
конечных кристаллических многогранниках все
элементы симметрии проход€т через одну
неподвижную (фиксированную) точку Ч точку
пересечени€ кристаллографических осей (т.е.
через начало координат). Ќыне пользуютс€
преимущественно терминами "вид симметрии"
(в.с.) Ч ему отдаетс€ предпочтение в русской
минералого-кристаллографической литературе Ч
или "класс симметрии", который более
употребителен за рубежом. «аметим, что в
кристаллах 32 вида симметрии естественным
образом подраздел€ютс€ по уровню симметрии на 3
категории:
- низша€ (наименее симметрична€) Ч без
главной оси высокого (выше 2-го) пор€дка; могут
присутствовать от одной до трех двойных осей;
включает 8 в.с;
- средн€€ (более симметрична€) Ч с одной
главной осью 3-го, 4-го или 6-го пор€дка,
ориентированной вертикально, т.е. вдоль
кристаллографической оси с, включает 19 в.с.
- высша€ (сама€ высокосимметрична€) Ч с трем€
главными ос€ми 4-го пор€дка (простыми или
инверсионными) либо с трем€
взаимноперпендикул€рными ос€ми 2-го пор€дка, но в
любом случае об€зательно с четырьм€ ос€ми 3-го
пор€дка; включает 5 в.с.
<<< √еометрические
формы кристаллов | —одержание
| —ингони€, или кристаллографическа€
система >>>
ѕознакомитьс€ с изображени€ми и описани€ми других объектов природы –оссии и сопредельных стран -
 минералов и горных пород, минералов и горных пород,
 почв, почв,
 грибов, грибов,
 водорослей, водорослей,
 лишайников, лишайников,
 листостебельных мхов, листостебельных мхов,
 деревьев, кустарников, кустарничков и лиан, деревьев, кустарников, кустарничков и лиан,
 трав€нистых растений (цветов), трав€нистых растений (цветов),
 €год и других дикорастущих сочных плодов, €год и других дикорастущих сочных плодов,
 водных беспозвоночных животных, водных беспозвоночных животных,
 насекомых-вредителей леса, насекомых-вредителей леса,
 дневных бабочек, дневных бабочек,
 пресноводных и проходных рыб, пресноводных и проходных рыб,
 земноводных (амфибий), земноводных (амфибий),
 пресмыкающихс€ (рептилий), пресмыкающихс€ (рептилий),
 птиц, птичьих гнезд, их €иц и голосов, а также птиц, птичьих гнезд, их €иц и голосов, а также
 млекопитающих (зверей), -
можно в разделе ѕрирода –оссии нашего сайта. млекопитающих (зверей), -
можно в разделе ѕрирода –оссии нашего сайта.
¬ разделе ѕрирода в фотографи€х
размещены также тыс€чи научных фотографий грибов, лишайников, растений и
животных –оссии и стран бывшего ———–, а в разделе
ѕриродные ландшафты мира - фотографии природы
 ≈вропы, ≈вропы,
 јзии, јзии,
 —еверной и —еверной и
 ёжной јмерики, ёжной јмерики,
 јфрики, јфрики,
 јвстралии и Ќовой «еландии и јвстралии и Ќовой «еландии и
 јнтарктики. јнтарктики.
¬ разделе ћетодические материалы
¬ы также можете познакомитьс€ с описани€ми разработанных экологическим центром "Ёкосистема"
печатных определителей растений средней полосы,
карманных определителей объектов природы средней полосы,
определительных таблиц "√рибы, растени€ и животные –оссии",
компьютерных (электронных) определителей природных объектов,
полевых определителей дл€ смартфонов и планшетов,
методических пособий по организации проектной де€тельности школьников и полевых экологических исследований
(включа€ книгу дл€ педагогов " ак организовать полевой экологический практикум"), а также
учебно-методических
фильмов по организации проектной исследовательской де€тельности школьников в природе.
ѕриобрести все эти материалы можно в нашем некоммерческом »нтернет-магазине.
“ам же можно приобрести mp3-диски √олоса птиц средней полосы –оссии и
√олоса птиц –оссии, ч.1: ≈вропейска€ часть, ”рал, —ибирь.
|







